Peterson mutual exclusion algorithm:
The system is described in a Simple Programming Language:
peterson : SYSTEM
s : VAR bool WHERE s=false
BEGIN
comp1 : PROGRAM
y1 : VAR bool WHERE y1=false
BEGIN
WHILETRUE DO
[y1,s] := [true,true] ;;
AWAIT ((not y2) or (not s)) ;;
y1 := false
OD
END comp1
||
comp2 : PROGRAM
y2 : VAR bool WHERE y2=false
BEGIN
WHILETRUE DO
[y2,s] := [true,true] ;;
AWAIT ((not y1 ) or s) ;;
y2 := false
OD
END comp2
END peterson
This system is translated automatically into the following transition system:
peterson: SYSTEM
BEGIN
s : VAR bool
BEGIN
comp1 : PROGRAM
BEGIN
y1 : VAR bool
BEGIN
"Req_1"
1:: TRUE ---> y1 ::= true ,
s ::= true
GOTO 2 []
"In_1"
2:: ( ( not y2 ) or ( not s ) ) ---> GOTO 3 []
"Out_1"
3:: TRUE ---> y1 ::= false
GOTO 1 []
END
END comp1
||
comp2 : PROGRAM
BEGIN
y2 : VAR bool
BEGIN
"Req_2"
1:: TRUE ---> y2 ::= true ,
s ::= false
GOTO 2 []
"In_2"
2:: ( ( not y1 ) or s ) ---> GOTO 3 []
"Out_2"
3:: TRUE ---> y2 ::= false
GOTO 1 []
END
END comp2
END
INITIALLY :
s = false and
y1 = false and
y2 = false and
pc2 = 1 and
pc1 = 1
END peterson
The property we want to prove is
not (pc1=3 and pc2=3)
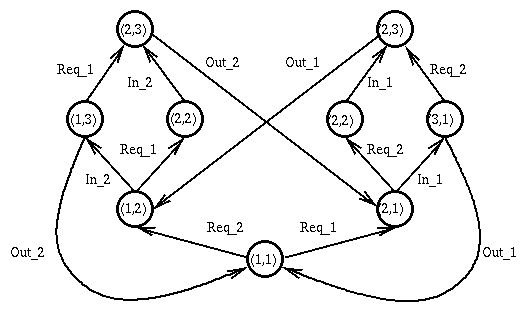
The following abstract state graph is constructed for the bakery system using
the predicate: y1, y2 and s.
The control configuration (3,3) which violate mutual exlusion
property is not reachable.
Back to the Invariant Checker home page
