An alternating bit protocol:

We consider an alternating bit protocol where sent messages are memorized. the sent messages are sequences of integers.

alternating_bit : SYSTEM 

BEGIN
 
IMPORTING alternating_bit_declarations

flagm,flagack : VAR bool

     BEGIN 

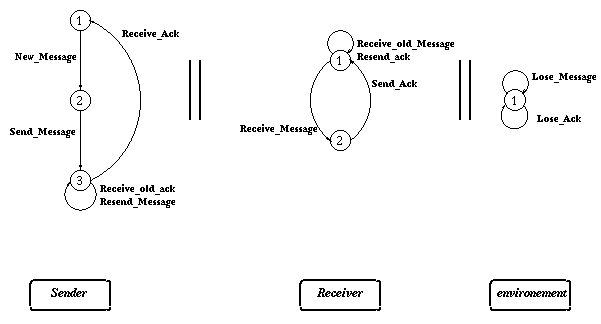
sender : PROGRAM
BEGIN
 b : VAR bool
 NB_mess : VAR massage
 Cm : VAR message_channel
 SIN : VAR message_list
BEGIN
"New_Message"
1::  true  
            ---> NB_mess  ::= NB_mess + 1 ; 
                 b ::= (not b) ; 
                 SIN ::= cons(NB_mess,SIN)  
GOTO 2 []

"Send_Message"
2::  true  
         ---> 
      Cm ::= (car(SIN),b) ; 
      flagm ::= true 
GOTO 3 []

"Resend_Message"
3::  not (flagack and Cack = b)  
               --->  
        Cm ::= (car(SIN),b) ; 
        flagm ::= true 
GOTO 3 []

"Receive_Ack"
3::   flagack and Cack = b 
        --->  
  GOTO 1 []

END
END sender


||


receiver : PROGRAM
BEGIN
c : VAR bool
OUTR : VAR nat
Cack : VAR bool
ROUT : VAR message_list
BEGIN

"Receive_old_message"
1:: (not flagm ) or  getbit(Cm)=c  
                 ---> 
           Cack ::=c ; 
           flagack ::= true 
GOTO 1 []

"Receive_Message"
1::  flagm  and getbit(Cm)/=c  
                  --->  
               OUTR::=getmess(Cm) ;
               ROUT ::= cons(getmess(Cm),ROUT) 
GOTO 2 []

"Send_Ack"
2:: true  ---> 
               flagack ::= true ;
               Cack ::= (not c) ; 
               c::= (not c) 
 GOTO 1 []
END
END receiver

||

env : PROGRAM
BEGIN
BEGIN
"LOSE_MESSAGE"
1::  true 
           --->  flagm ::= false 
 GOTO 1 []

"LOSE_ACK"
1::  true   
           ---> flagack ::= false GOTO 1 []
END
END env

       END 

  INITIALLY   :    
                   flagm = true and flagack = true
                   and b=false and c=false
                   and OUTR=0 and NB_mess = 0
                   and Cm = (0,b)
                   and Cack = false
                   and pc1=1 and pc2=1 and pc3=1
                   and SIN=null and ROUT= null
 END alternating_bit

The PVS imported theory alternating_bit_declarations contains the following declarations:

alternating_bit_declarations  : THEORY

  BEGIN
  message : TYPE = nat
  message_channel : TYPE = [message,bool]
  message_list  : TYPE = list[message]

  getmess(C:message_channel):message = proj_1(C)
  getbit(C:message_channel):bool = proj_2(C)
 
 END alternating_bit_declarations

Using abstraction techniques, the following abstract state graph is generated automatically. The abstract state is defined using the predicates

 P1 : getbit(Cm)=c

and

 P2 :Cack=b

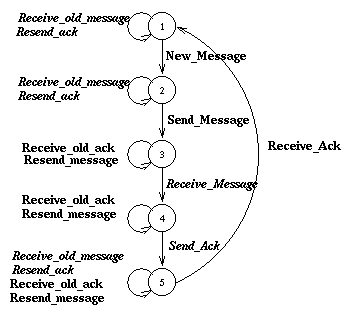
There are five abstract states, where each state is a record : [#control,valuation(P1,P2)#]:

state 1 : [# control   =  (1, 1, 1)
             valuation = p1 and p2  #]

state 2 : [# control   =  (2, 1, 1)
             valuation = p1 and (not p2)  #]

state 3 : [# control   =  (3, 1, 1)
             valuation = (not p1) and (not p2)  #] 

state 4 : [# control   =  (3, 2, 1)
             valuation = (not p1) and (not p2)  #]  

state 5 : [# control   =  (3, 1, 1)
             valuation =  p1 and p2  #]

The global control configuration (2, 2, 1) (that is, pc1 = 2 and pc2 = 2 and pc3 = 1) is not reachable.

An alternating bit protocol:

Back to the Invariant Checker home page